Description

In this work, Ramachandran probability distributions are presented for residues in protein loops from a high-resolution data set with filtering based on calculated electron densities. Distributions for all 20 amino acids (with cis and trans proline treated separately) have been determined, as well as 420 left-neighbor and 420 right-neighbor dependent distributions. The neighbor-independent and neighbor-dependent probability densities have been accurately estimated using Bayesian nonparametric statistical analysis based on the Dirichlet process. In particular, we used hierarchical Dirichlet process priors, which allow sharing of information between densities for a particular residue type and different neighbor residue types. The resulting distributions have been tested in a loop modeling benchmark, and are shown to improve protein loop conformation prediction significantly.

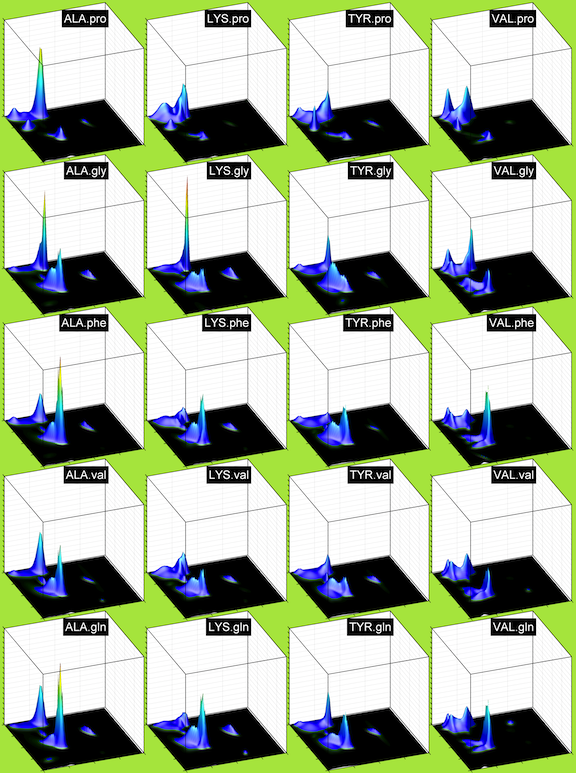
In the figure above, XXX.yyy indicates the Ramachandran distribution of residue type XXX with right neighbor yyy. In this file (35 MByte pdf, 43 pages), we show the Ramachandran distributions for the TCBIG set (Turns+Coil+Bridge+PiHelix+310Helix). yyy.XXX indicates the Ramachandran distribution of residue XXX with left neighbor yyy. The first page shows the neighbor-independent distributions.

---

License

As of November 8, 2019, it is based on a Creative Commons CC BY 4.0 license. The license for the 2010 backbone-dependent rotamer library is now less restrictive than it was previously. It is the same for both academia and industry: The library is free, redistributable, and modifiable as long as you acknowledge the source of the library. See details in the link.

License

---

Usage

Each file contains probabilities of phi,psi for specific residue types given the residue type of a neighbor to the left or to the right. "ALL" means all neighbor residues of the residue in question were kept in the calculation. The format is this:

So for instance, here are some lines for LEU-right-PRO Ramachandran distribution

Res Dir. Neigh phi psi Probability log(prob) Cumulative_sum
LEU right PRO -175 -130 5.237406e-08 16.76485 2.082167e-04
LEU right PRO -175 -125 4.726758e-08 16.86744 2.082640e-04
LEU right PRO -175 -120 4.449988e-08 16.92778 2.083085e-04
LEU right PRO -175 -115 4.332896e-08 16.95444 2.083518e-04
LEU right PRO -175 -110 4.208621e-08 16.98355 2.083939e-04
LEU right PRO -175 -105 3.898562e-08 17.06007 2.084329e-04
LEU right PRO -175 -100 3.459067e-08 17.17968 2.084675e-04

Res = the residue type for the Ramachandran Distribution

Dir = the direction of the neighbor ("ALL" is ALL residue types at once)

phi and psi = the floors of 5x5 regions

Probability = the probability in the 5x5 regions with floor at that phi,psi (e.g. the point at -175,-130 covers the range (-175,-130) to (-170,-125)

log(prob) = followed by the log probaility.

Cumulative_sum = the cumulative sum and can be used for drawing random values from the probability distributions. The sum is 1.0 for each neighbor map.

CPR is cis proline as a central amino acid

Note: the probabilities cover the regions above and to the right of the phi,psi point; e.g., at phi,psi = {60,0}, the probability is for the region {60,0} -> {65,5}.

To calculate probabilies for triplets, use:

To calculate probabilies for triplets (center,left,right), use:

log p*(phi,psi | C,L,R) = log p(phi,psi |C,L) + log p(phi,psi |C,R) - log p(phi,psi |C,R=ALL)

Once log p*(phi,psi | C,L,R) is calculated, calculate p*(phi,psi |C,L,R) = exp(log(p*(phi,psi | C,L,R)))
Then sum them up for each Ramachandran map, and normalize the probabilities by dividing by the sum:

p(phi,psi, | C,L,R) = p*(phi,psi | C,L,R) / sum

There are four distribution files:
NDRD_TCBIG.txt = data from Turn, Coil, Bridge, PiHelix, and 310 Helix
NDRD_TCB.txt = data from Turn, Coil and Bridge
NDRD_Conly.txt = Coil only
NDRD_Tonly.txt = Turn only

---