Introduction

Basics

A torsion angle or dihedral angle is the angle between two planes. For four consecutively bonded atoms A-B-C-D, atoms A-B-C define the first plane and atoms B-C-D define the second plane. The angle between these two planes (A-B-C and B-C-D) is a dihedral or torsion angle. The positive rotation is the clockwise rotation of the vector C-D relative to the vector A-B when looking in the direction of the B-C vector: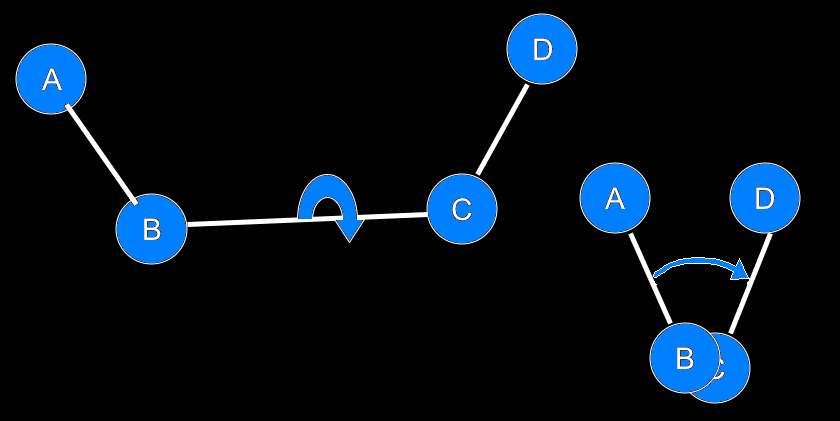

When all 4 atoms lie in the same plane and A and D atoms are on the same side relative to B-C vector, the torsion angle is zero: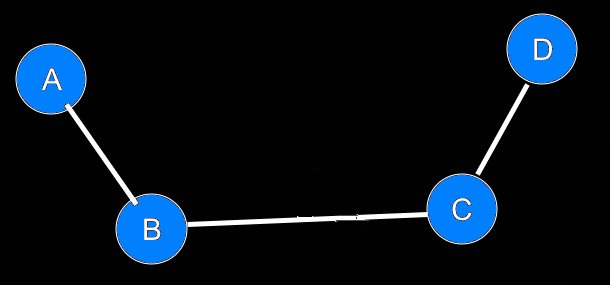

If they are on opposite sides then the angle is 180° or -180°: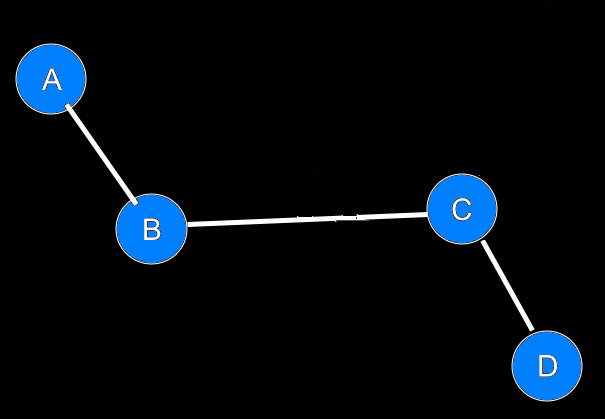

The torsion angle, A-B-C-D only alters the distance between atoms A and D; the other interatomic distances are constrained by approximately constant bond lengths and bond angles.

The backbone torsion angles are ω, φ and ψ. The φ dihedral angle for residue i is defined by C_i-1-N_i-Cα_i-C_i; the ψ dihedral angle for residue i is defined by N_i-Cα_i-C_i-N_i+1; the ω dihedral angle for residue i is defined by Cα_i-1-C_i-1-N_i-Cα_i. ω is almost always near 180°; although there is some variation dependent on the values of ψ_i-1 and φ. For more details, click here.

The side-chain torsion angles, χ₁, χ₂, χ₃ and χ₄ define a side-chain conformation. For example, in the case of lysine, χ₁ is N-Cα-Cβ-Cγ and defines a rotation around the Cα-Cβ bond. χ₂ is Cα-Cβ-Cγ-Cδ and defines a rotation around the Cβ-Cγ bond. χ₃ is Cβ-Cγ-Cδ-Cε and defines a rotation around the Cγ-Cδ bond. χ₄ is Cγ-Cδ-Cε-Nζ and defines rotation around the Cδ-Cε.

Traditional Rotamer Library

Most side-chain χ torsion angles, are centered on sp3-sp3 hybridized bonds, and exhibit three narrow, approximately symmetric peaks in their probability density distributions. For example, here is the backbone-independent density for methionine χ₁: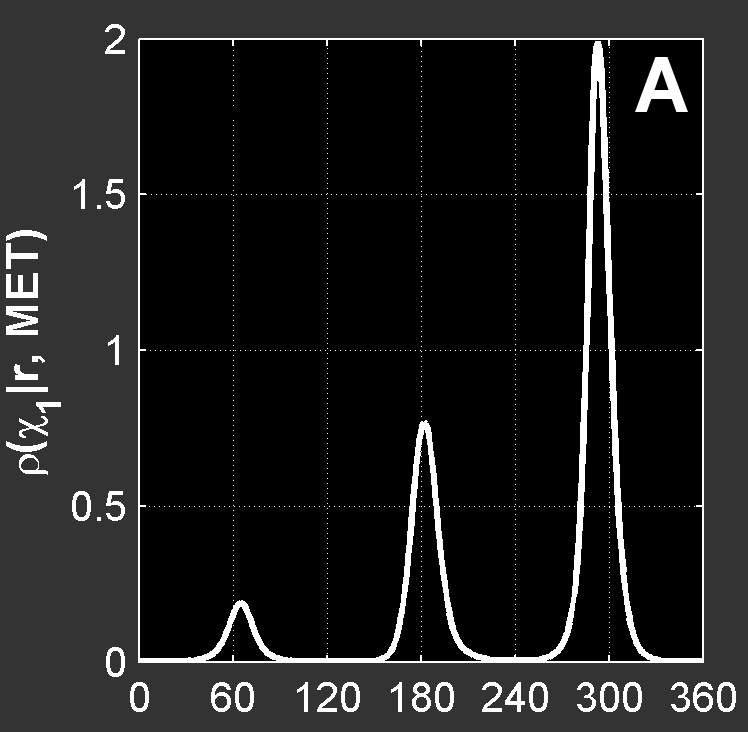

MET χ₁ has gauche+ (g+), trans (t), and gauche- (g-) peaks at approximately 60°;, 180°, and 300° respectively. 300° for g- is the same as -60°. The location and shape of these peaks vary somewhat (by at most 20°) a residue backbone conformation changes, and their standard deviations are at usually less than 10° in high-resolution structures. It therefore makes sense to define a set of discrete side-chain conformations (χ₁, χ₂, χ₃ and χ₄), also known as rotamers. We refer to such χ degrees of freedom as rotameric. The prevailing majority of side-chain χ angles are rotameric, comprising the following:

ARG χ1, χ2, χ3, χ4    HIS χ1                PRO χ1
             ASN χ1                ILE χ1                SER χ1
             ASP χ1                LEU χ1, χ2            THR χ1
             CYS χ1                LYS χ1, χ2, χ3, χ4    TRP χ1
             GLN χ1, χ2            MET χ1, χ2, χ3        TYR χ1
             GLU χ1, χ2            PHE χ1                VAL χ1
             

Nevertheless, not all side-chain χ angles adhere to a concept of a rotamer. Non-rotameric degrees of freedom in protein side chains are centered on sp3-sp2 bonds, and exhibit broad and often asymmetric probability density distributions. These non-rotameric degrees of freedom exist in ASN, ASP, GLN, GLU and the aromatic amino acids PHE, TYR, HIS and TRP. Each of these residue types has one or two (in the case of GLN and GLU) rotameric degrees of freedom nearer the backbone, while the terminal degree of freedom is non-rotameric. The shape and location of the distributions of these non-rotameric dihedral angles vary depending on the backbone conformation and the rotamer of the non-terminal degrees of freedom. As examples, we show the backbone-independent χ₂ probability densities for asparagine and tryptophan for each of the three χ₁ rotamers (<g+>, <t>, <g->) of these residue types and χ₃ densities for all 9 χ₁, χ₂ rotamers of glutamine (<g+, g+>, <g+, t>, ... and <g-, g->):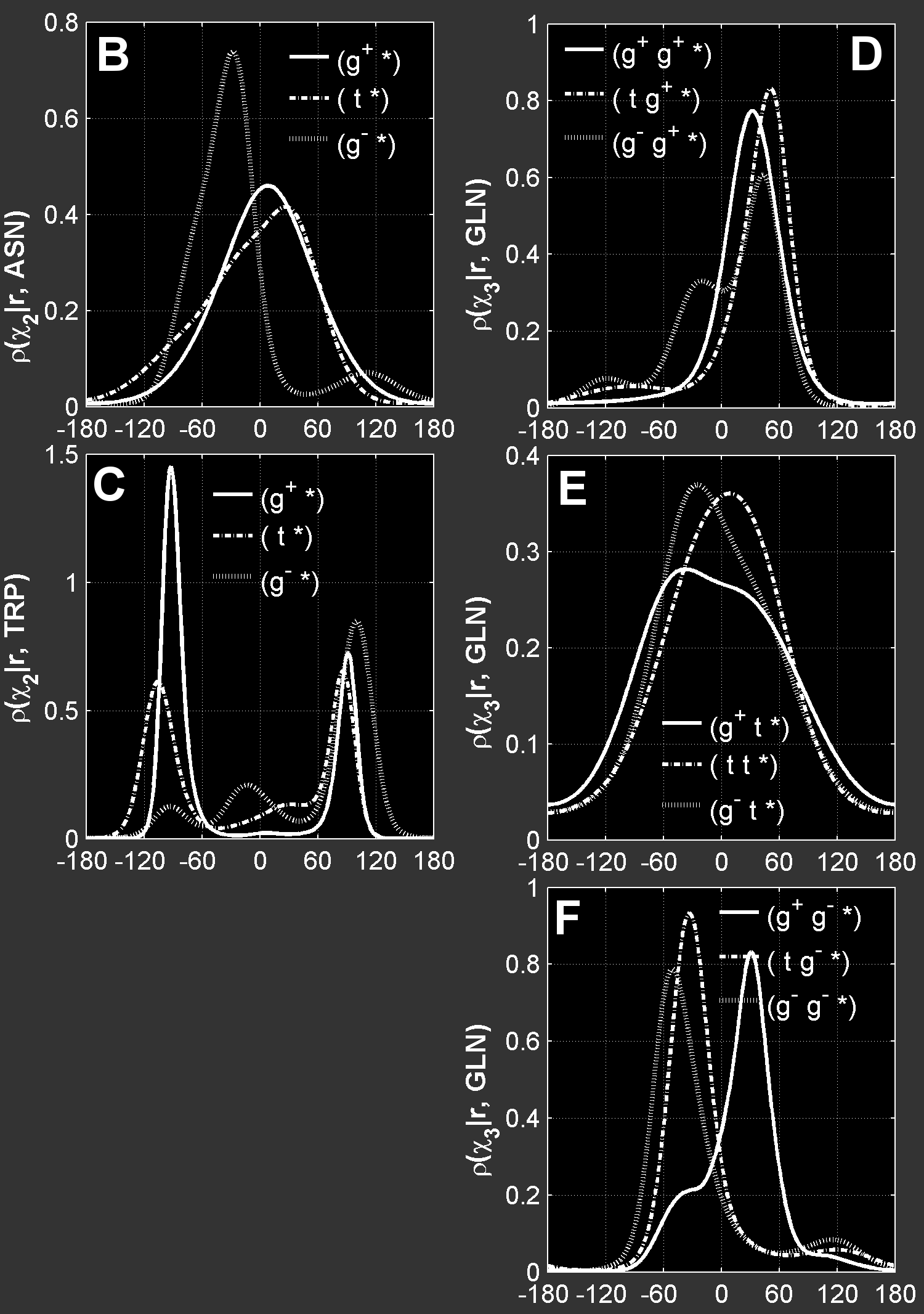

Here is a gif animation illustrating how χ₂ density varies as a function of φ and ψ for the trans χ₁ rotamer of ASN. The Ramachandran density for the trans χ₁ of ASN is shown in the inset in the top-right corner, ρ(φ, ψ | r = <t>) showing the major secondary-structure conformational regions: α-helix, antiparallel β-sheet, parallel β-sheet and left-handed helix. A brighter color corresponds to a higher density. The red box on the inset figure and the numeric values in the title indicate the current backbone conformation (φ, ψ). As the backbone conformation changes we can see several different χ₂ populations dominating in different (φ, ψ) regions. The positions of their maximum values move with φ and ψ and sometimes they coalesce into a single wide population. You can watch movies for all non-rotameric degrees of freedom here.

The non-rotameric degrees of freedom are:

ASN χ2    GLN χ3    PHE χ2    HIS χ2
             ASP χ2    GLU χ3    TYR χ2    TRP χ2
             

Under the term "traditional rotamer library", we mean a library of discrete side-chain conformations only, i.e. rotamers. The traditional rotamer library includes: rotamer frequencies, their mean torsion angles and standard deviations. These values vary significantly as a residue backbone conformation changes. Therefore, a traditional backbone-dependent rotamer library contains values for rotamer frequencies, mean χ angles and standard deviations as a function of the backbone torsion angles, φ and ψ.

In this traditional rotamer model, each side-chain χ has a set of discrete conformations, i.e. rotamers. For instance, serine has only one degree of freedom, χ₁. Its χ₁ has 3 rotamers with mean values about +60°, 180° and -60°. Therefore, for serine there are 3 rotamers in total: <g+>, <t> and <g->. In contrast, leucine has two side-chain degrees of freedom, i.e. χ₁ and χ₂. Each of them has its own 3 rotamers, g+, t and g-, producing 3 × 3 = 9 rotamers in total: <g+, g+>, <g+, t>, <g+, g->, <t, g+>, <t, t>, <t, g->, <g-, g+>, <g-, t> and <g-, g->.

We can designate g+, t and g- rotamers as 1, 2 and 3 respectively for serine χ₁, leucine χ₁ and leucine χ₂. Thus serine has <1>, <2> and <3> rotamers while leucine has <1, 1>, <1, 2>, ..., <3, 3>. We can use the same number designations for the rotamers of the 18 standard amino acids with flexible side chains. For example, arginine and lysine have 3 × 3 × 3 × 3 = 81 rotamers in total (<1, 1, 1, 1>, <1, 1, 1, 2> ... <3, 3, 3, 3>). For the non-rotameric degrees of freedom, the angular space can be divided into some number of bins to approximate a rotamer model. For example, for ASN χ₂ in 1997 we used three rotamers to represent the dihedral angle distribution. In 2002, we expanded this to six rotamers for χ₂, so ASN had 3 × 6 = 18 (<1, 1>, <1, 2>, ... <3, 6>) rotamers. For the 2010 rotamer names, definitions and total counts of 18 amino acids please refer to the table below:

^* TPR (trans proline), CPR (cis proline) and CYH (non-disulfide-bonded Cys), CYD (disulfide-bonded Cys) percentages are calculated relative to the total number of PRO and CYS respectively. Each rotameric degree of freedom, χ has the rotamer definitions: g+ = [0°, 120°), t = [120°,240°), g- = [240°,360°). ^† PRO, CPR, and TPR have only g+ and g- rotamers.

In the new, 2010 library, we strictly distinguish between rotameric and non-rotameric degrees of side-chain freedom based on the hybridization state of the atoms involved in a corresponding torsion angle, χ.

2010 Library

Aims and Features

There were several aims in deriving a new backbone-dependent rotamer library:

1. taking advantage of the much larger dataset that is available now than at the time of the last library (2002)
2. using electron density calculations to remove highly dynamic side chains (or protein segments) that have uncertain conformations or coordinates (Shapovalov and Dunbrack, 2007)
3. deriving accurate and smooth density estimates of rotamer populations and their relative frequencies, including rare rotamers, as a continuous function of backbone dihedral angles
4. deriving smooth estimates of the mean values and variances of rotameric side-chain dihedral angles
5. improving the treatment of non-rotameric degrees of freedom, i.e. those are not well described by the rotamer model
6. employing methods producing meaningful estimates of rotamer frequencies, dihedral angles means and variances in the Ramachandran areas lacking experimental data.

We applied adaptive kernel density estimates to compute backbone-dependent probabilities of side-chain rotamers and adaptive kernel regression to estimate backbone-dependent mean χ angles and their standard deviations. The central concept of these methods is to put a bell-shaped curve, i.e. a kernel function on top of each experimental data point from a data set. This action converts a set of discrete data points to a set of continuous objects, i.e. smooth functions. The bell-shaped curve has a bandwidth which locally adapts depending on the amount of available data. Since we are deriving for rotamer probabilities, means and standard deviations as a function of φ and ψ, we used the periodic von Mises probability distribution as the kernel choice rather than Gaussians or other non-periodic kernels. For the non-rotameric degrees of freedom, we developed an innovative adaptive kernel regression of adaptive kernel density. Here we place a kernel on top of each experimental data point not only in φ and ψ space but also in χ space in such a way that for any φ and ψ a combination of χ kernels leads to a local estimate of χ probability density. We chose an appropriate method to adapt these kernels in the φ,ψ space and χ space as well to produce statistically sound estimates and at the same time not to lose local details of the side chain model. For a complete description of the methods, please click here.

We developed methods that enable estimation estimation of rotamer statistics or non-rotameric χ density as continuous function of φ and ψ, i.e. at any numerical values of φ and ψ. However, we evaluated the rotamer probabilities and angle statistics on a 10° grid in φ and ψ in order to provide a rotamer library that would be compatible with methods that require a fast lookup of these values, such as Rosetta or SCWRL. The text files (which can be converted to binary files) are a good trade-off between memory overhead and experimental precision in structures. The advantages are backward compatibility, relatively low memory overhead, no CPU overhead, no restriction to a particular platform, operating system, computer language. There are several disadvantages. Users have to implement their own parsers. There is reduced accuracy of the estimated statistics at points not on the grid and decreased accuracy of derivatives when these are calculated from neighboring grid values. In the future, we will provide code that produces rotamer statistics at any value of φ and ψ, but this requires significant optimization and accurate numerical methods for derivative computation, etc.

2010: Traditional Rotamer Model Vs. New Model of χ Densities

In 2010 we provide two different types of backbone-dependent side-chain models: 1) the traditional rotamer model as in 1997 and 2002 for both rotameric and non-rotameric degrees of freedom (in 30° bins); 2) the traditional model for the rotameric degrees of freedom but also full probability density estimates for the non-rotameric degrees of freedom as a function of φ and ψ. The traditional model provides support for existing applications. Its format has remained the same as the 2002 libraries. While the traditional 2010 library demonstrates improved performance over the 2002 library, there are applications where a backbone-dependent model of χ densities may provide increased accuracy. It is also possible to use both, the traditional rotamer library in the first stage of modeling and full χ densities at the second, refinement stage.

For a definition and description of Traditional Rotamer Library, see above.

The traditional backbone-dependent rotamer library is available as a single larger file. There are 18 standard amino acid types with (glycine and alanine do not have flexible side chains). There are three choices to make:

• Choice #1: subclasses for proline and cysteine or not
  • PRO is a single category trans or cis. CYS is a single category whether or not disulfide-bonded.
    In total 18 residue categories.
  • PRO has 3 categories: TRP (trans PRO), CPR (cis PRO) and PRO (TRP+CPR).
    CYS has 3 categories: CYH (non-disulfide-bonded CYS), CYD (disulfide-bonded CYS) and CYS (CYH+CYD).
    In total 22 residue categories.
  
  
• Choice #2: rotamer bins for 8 non-rotameric χ are
  • backbone-dependent - vary with φ, ψ such that the mode is the center of a bin
  • backbone-independent - fixed for all φ, ψ
  
  
• Choice #3: the level of smoothness of the rotamer library. 0% contains the optimized kernel width according to the maximum log likelihoods, while 2%, 5%, 10%, 20% and 25% are increasing levels of smoothness. The 5% libraries represent a good trade-off of rotamer detail and smoothly varying probabilities and dihedral angles:
  • 5% (default choice)
  • 0%
  • 2%
  • 10%
  • 20%
  • 25%

A user decides whether additional subclasses are needed for proline and cysteine in their specific applications. While the differences between trans PRO and cis PRO or between non-disulfide-bonded and disulfide-bonded CYS are not as drastic as between different residue types, they are still significant and may lead to improved accuracy.

As discussed above, the density distributions for the non-rotameric χ angles demonstrate backbone dependence, i.e. the shape and location of the density peaks significantly vary as φ and ψ change. For this reason the "rotamer" definitions, i.e. their left and right limits vary as a function of φ and ψ. We provide two options. The first option has dynamic or backbone-dependent "rotamer" definitions for the 8 non-rotameric χ angles. The second option has static or backbone-independent "rotamer" definitions. In applications where a user does not care about assigning a rotamer type to an experimental side-chain conformation or does not need to calculate rotamer-specific derivatives, the first option with backbone-dependent "rotamer" definitions is preferable, since the mode of the distribution is centered in the maximum probability bin. In contrast, for the applications where a user wants to query a likelihood of some side-chain conformation or wants a rotamer, for example GLN <1,3,7> to remain the same, i.e. with the same left and right limits, the second choice with the backbone-independent definitions is desirable. We provide 8 small files for each non-rotameric χ with these backbone-independent definitions.

As shown above, the statistical methods used in the 2010 library are completely different from the ones used in 1997 or 2002. The 1997 and 2002 libraries relied on Bayesian formalism while the 2010 library takes advantage of adaptive kernel density estimates, kernel regressions and adaptive kernel regressions of densities. These kernel methods were chosen to produce smoother and more accurate libraries than in 1997/2002. The level of smoothness was separately optimized for each residue type, each degree of freedom and each library component. However, the library consists of many different components and the final performance is an interplay of separate components. Our benchmark tests in SCWRL4 and Rosetta demonstrated the additional 5% smoothness lead to improved accuracy in these applications. The 5% library is our suggested, default choice. Nevertheless, there are some applications where a user can benefit from increased or decreased smoothness. Additional testing is required for such applications. For example, there is a scenario when a user may introduce the smoothest, 25% library in initial modeling and at the final stage of modeling during the refinement switch to 0% library with the greatest amount of details.

For the 8 non-rotameric χ angles, we developed a new model describing their internal properties in a statistically more appropriate way. Each non-rotameric χ is modeled with one-dimensional probability density distribution varying as a function of the backbone φ and ψ. The non-rotameric χ is always the last χ in these side-chain types, i.e. χ_n; the preceding χ angles are rotameric, i.e. χ₁, χ₂, ... χ_n-1. There are therefore N_tot = N₁ × N₂ × ... × N_n-1 rotamers for each side chain with a non-rotameric degree of freedom. Separately for each of the N_tot rotamers, we estimated the χ_n probability density as a function of φ and ψ, i.e. ρ(χ_-n | r, φ, ψ).

The remaining residue types with all rotameric χ angles are modeled as a Traditional Rotamer Library. Their rotamer model allows for quick traversal through discrete side-chain conformation space which is a good statistical model for sp3-sp3 hybridized bonds.

In future we may consider modeling all χ angles (whether rotameric or non-rotameric) for all residue types as backbone-dependent χ densities along with the traditional rotamer model which obviously has advantages in exhaustive searches of conformation space.

The new model of χ densities has separate file(s) for each residue type. For each rotameric residue type there is always a single file with backbone-dependent rotamer probabilities (Traditional Rotamer Model). For each non-rotameric residue type we provide three files. The first file contains the χ Densities. The second and third files purely belong to Traditional Rotamer Model. They are provided for convenience, so that the user can easily switch between two models for the non-rotameric residue types if needed.

1. A text file with χ_n densities as a function of φ, ψ and rotamer, r_-n = 1, 2 ... N₁ × N₂ × ... × N_n-1 along with backbone-dependent rotamer probability for each such rotamer, r_-n.
2. A text file with backbone-dependent rotamer probabilities for all "rotamers", r = 1, 2 ... N₁ × N₂ × ... × N_n-1 × N_n.
3. A small text file with backbone-independent χ_n "rotamer" definitions used in 2.

14:
                 ARG, ILE, LEU, LYS, MET, SER, THR, VAL
                 CYS, CYH, CYD
                 PRO, TPR, CPR

             
8:
                 ASN, ASP, GLN, GLU, HIS, PHE, TRP, TYR

• 5% (default choice)
• 0%
• 2%
• 10%
• 20%
• 25%

Format

General

Depending on what library model a user chooses from a list, several files in different text formats are available from a distributive package. The names and formats of the files are self-explanatory. A header of each file describes what is included in a file and some important options and their values used in a generated library. When parsing a file, a user can always skip any commentary information by ignoring lines starting with "#":

# Backbone-dependent rotamer library with regular rotamers
             #
             # phi interval, deg	[-180.0, 180.0]
             # phi step, deg	10.0
             # psi interval, deg	[-180.0, 180.0]
             # psi step, deg	10.0
             #
             # Residue type	MET
             #
             # Rotamer probability precision	0.000001
             #
             # Number of chi angles (degrees of freedom)	3
             # Number of chi angles treated as discrete	3
             # Number of bins for each discrete chi angle	[3, 3, 3]
             # Number of rotamers for discrete chi angles	27
             # Number of chi angles treated as continuous	0
             #
             # TotalDatapointsNum	12240
             

The actual data is included on the lines not starting with "#". The library data are presented in a table form either space or tab delimited. The beginning of the table is preceded with a "#", commentary line showing self-descriptive titles for each of its columns:

ser.bbdep.rotamers.lib
             # T  Phi  Psi  Count    r1 r2 r3 r4 Probabil  chi1Val chi2Val chi3Val chi4Val   chi1Sig chi2Sig chi3Sig chi4Sig
             #
             SER  -180 -180    19     1  0  0  0  0.802596    68.0     0.0     0.0     0.0       8.1     0.0     0.0     0.0
             SER  -180 -180    19     2  0  0  0  0.197211  -175.4     0.0     0.0     0.0      10.1     0.0     0.0     0.0
             SER  -180 -180    19     3  0  0  0  0.000193   -62.9     0.0     0.0     0.0       8.6     0.0     0.0     0.0
             
             

asn.bbind.chi2.Definitions.lib
             # r1     r2     r3     r4     P         -logP     left       chi2      right
               1      1      0      0      0.236     1.443     -7.000     7.526     23.000
               1      2      0      0      0.195     1.634     23.000     36.529    53.000
             
             

asp.bbdep.densities.lib
             # T   Phi   Psi   Count   r1   Probabil   chi1Val   chi1Sig   -90          -85          -80          ...    85
             #
             ASP   -80   -10   404     3    0.630735   -68.8     7.7       4.505e-003   6.261e-003   8.664e-003   ...    3.256e-003
             ASP   -80   -10   404     1    0.342077   62.7      7.2       8.006e-003   1.022e-002   1.289e-002   ...    6.260e-003
             ASP   -80   -10   404     2    0.027188   -166.9    11.9      2.047e-002   1.350e-002   8.825e-003   ...    3.024e-002
             
             

"Traditional Rotamer Model" Package

When the 2010 library is used according to a traditional model of discrete conformations, i.e. rotamer model, there is a large text file with merged data for either 18 or 22 residue types (see above). We preserved the original format of the 1997 or 2002 text libraries in order to support older, existing applications:

ALL.bbdep.rotamers.lib
             # T  Phi  Psi  Count    r1 r2 r3 r4 Probabil  chi1Val chi2Val chi3Val chi4Val   chi1Sig chi2Sig chi3Sig chi4Sig
             #
             LEU   -70  -40  5884     3  2  0  0  0.668530   -68.3   173.0     0.0     0.0       6.5     8.1     0.0     0.0
             LEU   -70  -40  5884     2  1  0  0  0.296974  -177.4    58.8     0.0     0.0       7.2     6.1     0.0     0.0
             LEU   -70  -40  5884     3  1  0  0  0.014762   -88.5    60.0     0.0     0.0       7.7    10.2     0.0     0.0
             LEU   -70  -40  5884     2  2  0  0  0.009079  -175.1   153.0     0.0     0.0       9.3    10.0     0.0     0.0
             LEU   -70  -40  5884     3  3  0  0  0.007372   -89.0   -62.2     0.0     0.0       9.2    16.8     0.0     0.0
             LEU   -70  -40  5884     2  3  0  0  0.001641  -174.6   -78.6     0.0     0.0       9.5    11.9     0.0     0.0
             LEU   -70  -40  5884     1  1  0  0  0.001614    72.2    85.1     0.0     0.0       6.8     7.0     0.0     0.0
             LEU   -70  -40  5884     1  3  0  0  0.000020    70.3   -63.0     0.0     0.0       9.2    21.3     0.0     0.0
             LEU   -70  -40  5884     1  2  0  0  0.000009    72.1   165.9     0.0     0.0      10.1    13.3     0.0     0.0
             
             

T - three-letter designation of an amino acid type.

Phi - torsion angle value for backbone φ, C_i-1-N_i-Cα_i-C_i in a [-180, 180]° range.
Psi - torsion angle value for backbone ψ, N_i-Cα_i-C_i-N_i+1 in a [-180, 180]° range.
As in the previous versions of a rotamer library there is redundancy for reported values of backbone φ and ψ since both of them cycle from -180 up to 180 included. A user can ignore either -180 or 180 for φ and ψ or use the redundant values as checkpoints to catch possible parsing errors.
All statistics are provided exactly at the reported φ, ψ. For any φ, ψ off the grid points the neareast grid point can be used or a bilinear interpolation of the four nearest grid points.

Count - only to support the older text format: the number of (φ_i, ψ_i) experimental points from a data set within a 10° × 10° bin centered on the reported (φ, ψ). The data set is the set of experimental data used to generate the rotamer library.

r1 - a numerical designation of a χ₁ rotamer, i.e. 1, 2 .. N₁. When a residue type doesn't have χ₁, 0 is reported.
r2 - a numerical designation of a χ₂ rotamer, i.e. 1, 2 .. N₂. When a residue type doesn't have χ₂, 0 is reported.
r3 - a numerical designation of a χ₃ rotamer, i.e. 1, 2 .. N₃. When a residue type doesn't have χ₃, 0 is reported.
r4 - a numerical designation of a χ₄ rotamer, i.e. 1, 2 .. N₄. When a residue type doesn't have χ₄, 0 is reported.
The rotamer types are sorted according to their backbone-dependent probability, Probabil, see below.

Probabil - a probability of a rotamer, r = <r₁, r₂, r₃, r₄> given a backbone conformation (φ, ψ), i.e. P(r | φ,ψ). The sum of probabilities, P(r_j | φ,ψ) j = 1 .. N₁ × N₂ × N₃ × N₄, is always equal to 1 for any (φ, ψ).
Caution #1
Not all possible rotamer types may present in the table. If we did not have such a rotamer type in our experimental data set than its probability is absolute zero across all φ and ψ values. For such rotamer types there are no lines. Some rotamer types are so rare (a few data points in our data set) that they have 0.000000 probability reported for some (φ, ψ). Be cautious when using such rare rotamers, log(0.000000) may lead to NaN, -Inf and error exception. As a solution, a user may load all rotamers up to some threshold, for example up to 99.9%, 99%, 98% or 95%. It will help to resolve the log(0.000000) error and also ignore extremely rare and physically unrealistic rotamers and speed up your calculations.
Caution #2
The rotamer probabilities are simply frequencies of a set of possible side-chain conformations which add up to 1. These frequencies are backbone-dependent, i.e. vary as a function of a backbone conformation, (φ, ψ). A user can investigate any backbone conformation and have an estimate of the said side-chain conformation frequencies. However, a complete understanding has to be: most of the backbone conformations from Ramachandran map are merely physically impossible. They have large steric clashes with its own backbone and/or side chain. For such conformations a distribution of rotamer frequencies do not play a role, such backbone conformations cannot exist. For this reason, a rotamer library, i.e. a library of side-chain conformations cannot be used alone in applications involving backbone perturbation/modeling. When a protein backbone is not known, a Ramachandran probability has to be used in addition, i.e. a probability of a backbone conformation (φ, ψ) for some amino acid type, P(φ, ψ). P(φ, ψ) integrates to 1 over full ranges of φ and ψ. For downloading and learning more on neighbor-independent and neighbor-dependent Ramachandran probabilities, a user may refer to our study here.
Caution #3
The rotamer library should not be used in a way where all rotamers are treated equally, i.e. disregarding of their probabilities or energies. Either the probabilities should be used (as -log(Probabil)) or some other energy function should be used to distinguish the rotamers.

chi1Val - a mean value of a side-chain torsion angle, χ₁, reported for a given backbone conformation (φ, ψ) and rotamer, r = <r₁, r₂, r₃, r₄>. Most amino acid types have mean χ angles around the canonical 60°, 180° and -60° values. Due to an interaction of a side chain with its own backbone the mean χ values can deviate from the canonical ones. The reported χ angles demonstrate this. The mean χ₁ range is [-180, 180]°.
chi2Val - a mean value of a side-chain torsion angle, χ₂ with a range of [-180, 180]°.
chi3Val - a mean value of a side-chain torsion angle, χ₃ with a range of [-180, 180]°.
chi4Val - a mean value of a side-chain torsion angle, χ₄ with a range of [-180, 180]°.
Amino acid types not having χ₂ and/or χ₃ and/or χ₄ have 0.0 reported across the whole column.

chi1Sig - a standard deviation, i.e. sigma = sqrt(variance) of χ₁ for a given (φ, ψ) and rotamer, r. This standard deviation characterizes the width of χ spread around its mean χ value, chiVal. The χ spread width also varies as a function of a backbone, conformation (φ, ψ) owing to side chain-backbone interaction.
chi2Sig - a standard deviation of χ₂.
chi3Sig - a standard deviation of χ₃.
chi4Sig - a standard deviation of χ₄.
Amino acid types not having χ₂ and/or χ₃ and/or χ₄ have 0.0 reported across the whole column.

For each of the 8 non-rotameric χ_n we provide backbone-independent "rotamer" definitions, meaning the definitions are static and do not change as φ and ψ vary. Here is the format description based on glutamic acid:

glu.bbind.chi2.Definitions.lib
             # r1     r2     r3     r4     P         -logP     left       chi3      right
               1      1      1      0      0.406     0.900     5.500      20.276    35.500
               1      1      2      0      0.218     1.525     35.500     47.346    65.500
               1      1      3      0      0.072     2.631     65.500     78.259    95.500
               1      1      4      0      0.041     3.187    -84.500    -70.468   -54.500
               1      1      5      0      0.056     2.888    -54.500    -37.366   -24.500
               1      1      6      0      0.207     1.575    -24.500     -6.564     5.500
               2      1      1      0      0.423     0.860      6.500     21.331    36.500
               2      1      2      0      0.237     1.440     36.500     48.692    66.500
               2      1      3      0      0.081     2.512     66.500     78.719    96.500
               2      1      4      0      0.034     3.377    -83.500    -70.282   -53.500
               2      1      5      0      0.038     3.266    -53.500    -36.204   -23.500
               2      1      6      0      0.186     1.680    -23.500     -4.851     6.500
               3      1      1      0      0.350     1.049    -13.500      1.292    16.500
               3      1      2      0      0.240     1.427     16.500     29.564    46.500
               3      1      3      0      0.102     2.280     46.500     58.574    76.500
               3      1      4      0      0.038     3.273     76.500     89.996   106.500
               3      1      5      0      0.063     2.764    -73.500    -55.812   -43.500
               3      1      6      0      0.206     1.578    -43.500    -26.206   -13.500
             
             

r1 - a numerical designation of a χ₁ rotamer, i.e. 1, 2 .. N₁. When a residue type doesn't have χ₁, 0 is reported.
r2 - a numerical designation of a χ₂ rotamer, i.e. 1, 2 .. N₂. When a residue type doesn't have χ₂, 0 is reported.
r3 - a numerical designation of a χ₃ rotamer, i.e. 1, 2 .. N₃. When a residue type doesn't have χ₃, 0 is reported.
r4 - a numerical designation of a χ₄ rotamer, i.e. 1, 2 .. N₄. When a residue type doesn't have χ₄, 0 is reported.
The rotamer types are sorted according to their backbone-independent probability, P, see below.

P - a backbone-independent probability of a rotamer, r = <r₁, r₂, r₃, r₄>, i.e. P(r). The sum of probabilities, P(r_j), j = 1 .. N₁ × N₂ × N₃ × N₄, is equal to 1.

-logP - minus of log₁₀(P)

left - a left limit of a definition for a rotamer, r =<r₁, r₂, r₃, r₄>.
chi3 - a backbone-independent mean value for χ_n, i.e. χ₃ in the case of GLU, for the rotamer, r = <r₁, r₂, r₃, r₄>.
right - a right limit of a definition for the rotamer, r =<r₁, r₂, r₃, r₄>.

A χ_n rotamer definition is specified with an interval [left, right); any experimental χ_n point lying within this interval is said to be in such χ_n rotamer conformation.

"New Model of χ Densities" Package

In the package, "New Model of χ Densities" available for downloading, the rotameric residue types are always modeled with Traditional Rotamer Model. The only difference here is that they are provided as separate files for each type instead of one large merged file. A user can decide on which subclasses of proline or cysteine to use.

For each non-rotameric residue types, we provide three files:

Only one file comes from the New Model of χ Densities; it contains non-rotameric χ_n densities as a function of φ, ψ and rotamer r, r = 1, 2 ... N₁ × N₂ × ... N_n-1 along with backbone-dependent rotamer probability for each such rotamer, r. Its format is different but somewhat similar and described below.

The other two files belong to the Traditional Rotamer Model and contain backbone-dependent rotamer probabilities and backbone-independent non-rotameric χ_n definitions respectively. They are provided for convenience so that a user can switch between the Traditional Rotamer Model and the New Model of χ Densities for them. Their formats are the same and described above in Traditional Rotamer Model section of Format.

tyr.bbdep.densities.lib
             # T   Phi   Psi   Count   r1   Probabil   chi1Val   chi1Sig   -30          -25          -20          ...    145
             #
             TYR   -60   -40   1769    2    0.558459   -178.1    10.3      6.533e-004   6.394e-004   6.673e-004   ...    7.316e-004
             TYR   -60   -40   1769    3    0.418968   -72.7     11.3      3.303e-002   3.011e-002   2.714e-002   ...    3.616e-002
             TYR   -60   -40   1769    1    0.022572   75.1      12.6      6.880e-004   5.504e-004   4.554e-004   ...    9.006e-004
             
             

T - three-letter designation of an amino acid type.

Phi - torsion angle value for backbone φ, C_i-1-N_i-Cα_i-C_i in a [-180, 180]° range.
Psi - torsion angle value for backbone ψ, N_i-Cα_i-C_i-N_i+1 in a [-180, 180]° range.
As in the previous versions of a rotamer library there is redundancy for reported values of backbone φ and ψ since both of them cycle from -180 up to 180 included. A user can ignore either -180 or 180 for φ and ψ or use the redundant values as checkpoints to catch possible parsing errors.
All statistics are provided exactly at the reported φ, ψ. Using the new methods, there is no concept of a bin, so that the statistics are not estimated in a middle of bins.

Count - only as a reference to the older text format: the number of (φ_i, ψ_i) experimental points from a data set within a 10° × 10° bin centered on the reported (φ, ψ). The data set is the set of experimental data used to generate the rotamer library. The count also provides a practical understanding how many experimental data points were available within proximity of the reported (φ, ψ) at the time the library was compiled.

r1 - a numerical designation of a χ₁ rotamer, i.e. 1, 2 .. N₁.
r2 - a numerical designation of a χ₂ rotamer, i.e. 1, 2 .. N₂.
...
r(n-1) - a numerical designation of a χ_n-1 rotamer, i.e. 1, 2 .. N_n-1.
The rotamer types, r = 1, 2, ..., N₁ × N₂ × ... × N_n-1 are sorted according to their backbone-dependent probability, Probabil, see below.

Probabil - a probability of a rotamer, r = <r₁, r₂, ... r_n-1> given a backbone conformation (φ, ψ), i.e. P(r | φ,ψ). The sum of probabilities, P(r_j | φ,ψ) j = 1 .. N₁ × N₂ × ... × N_n-1, is always equal to 1 for any (φ, ψ).

chi1Val - a mean value of a side-chain torsion angle, χ₁, reported for a given backbone conformation (φ, ψ) and rotamer, r = <r₁, r₂, ... r_n-1>. The mean χ₁ range is [-180, 180]°.
chi2Val - a mean value of a side-chain torsion angle, χ₂ with a range of [-180, 180]°.
...
chi(n-1)Val - a mean value of a side-chain torsion angle, χ_n-1 with a range of [-180, 180]°.

chi1Sig - a standard deviation, i.e. sigma = sqrt(variance) of χ₁ for a given (φ, ψ) and rotamer, r.
chi2Sig - a standard deviation of χ₂.
...
chi(n-1)Sig - a standard deviation of χ_n-1.

glu.bbdep.densities.lib
             # Number of chi angles (degrees of freedom)	3
             # Number of chi angles treated as discrete	2
             # Number of bins for each discrete chi angle	[3, 3]
             # Number of rotamers for discrete chi angles	9
             # Number of chi angles treated as continuous	1
             

glu.bbdep.densities.lib
             # chi3 interval, deg	[-90.0, 90.0]
             # chi3 step, deg	5.0
           

glu.bbdep.densities.lib
             # T   Phi   Psi   Count   r1   Probabil   chi1Val   chi1Sig   -90          -85          -80          ...    85

Article

A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions.
Shapovalov, M.V., and Dunbrack, R.L., Jr., Structure 2011, 19, 844-858. Article